2.11 Statistic concepts and its application to detection

Radioactive decay is a phenomenon that can be described using probability distributions.

Each atomic disintegration during radioactive decay occurs completely independently of every other decay event, and the time interval between disintegrations is not constant. However, the average number of events, μ, that occurs in a specified time interval can be measured and considered as 'known'. At the same time, the probability of a disintegration to occur in an infinitesimally small time interval is nil.

All of these features are common to a Poisson's distribution P(x, μ), which serves to calculate the probability of having measured disintegrations (x) if the average of a large number of measurements is μ.

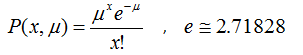
If the number of measured disintegrations is large (> 20), the distribution can be considered as Gaussian (or normal), which is symmetric and have the following properties:

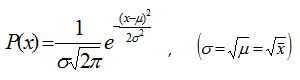
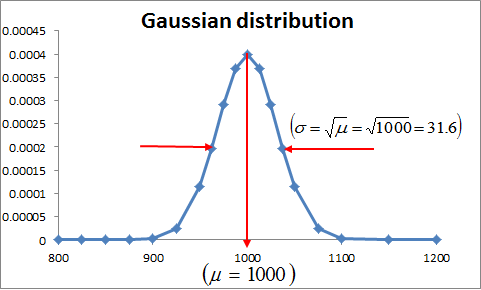
This property allows predicting the counting statistic error. The measuring time can be set as to achieve the acceptable relative error (RE) defined for a given measurement. Let’s assume that 10 % is the required precision for a measurement having a count rate n (s^-1). If the total counts are defined as N, then the measurement time needed can be calculated: